Detallant la resposta d'un circuit a una certa excitació (Objectiu principal del curs!)

Després d'un repàs dels exercicis setmanals i de com identificar i classificar les funcions de xarxa segons on tinguin els seus pols, hem respós la pregunta de : Quan durarà el règim transitori?

La resposta, que, lògicament només plausible en circuits estables en que les seves components pròpies tendeixin a convergir en un cert interval de temps t que serà major o menor depenent de la forma de la resposta pròpia (exponencial, constant....)

La duració del transitori, tindrà relació amb el temps que per conveni s'aproxima a uns 5 cops la constant de temps, era doncs igual a: 

•  D.Tr= 5/tau;

 Depenent del circuit tau variara, per exemple en un circuit de filtre paso bajo, tíndrem tau=RC,etc... 
També podem expressar la duració del transitori com l'invers de l'ample de banda (BW=Band Width)

Tot seguit ens hem plantejat com el PSPICE aconsegueix fer les gràfiques que hem fet en els últims exercicis sense saber derivar i per tant trobar quan val la sortida en funció de la entrada en un cert punt, el que fa és, aplicar la definició de derivada i anar agafant petits intervals que seran més o menys depenent de com de complexa sigui la excitació.

• Criteri per triar "Ts"----> Ts<Duració transitori /100

Finalment hem introduit una nova paraula al nostre vocabulari: "Discretitzar" que és el que fa el PSPICE, de manera que en un cert instant de temps nTs podem saber que vo(nTs) és igual a ella mateixa en un instant abans més la vg en nTs.
Per acabar hem realitzar una introducció al processat numèric (massa matemàtic) com a mostra d'aplicació d'un algoritme que permetés fer els càlculs discrets per determinar la gràfica. Hem vist que té una limitació si augmentem molt la freqüència de mostreig si el nostre PC no pot fer els càlculs a tanta velocitat.

Donat aquest problema, el criteri de Nyquist ens diu que :

                    Fmostreig>=2fmàx

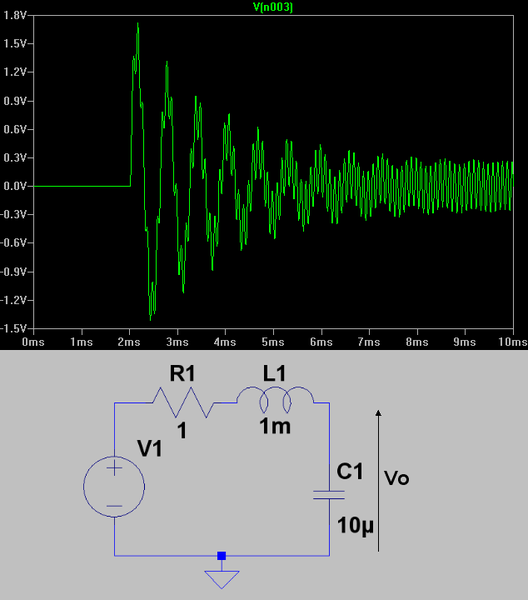Exemple del pas de règim transitori a permanent

Més Laplace

Avui, després d'un repàs breu sobre el que vam veure la classe passada, hem descrit com es "veurien" una R, una L i una C en el "món" del Laplace.

1. Un resistor R-->R
2. L-----> Ls-Li(0-)--->si tenim que l'excitació en t=0 és 0, llavors... L--> Ls
3. C----->Cs-V(0-)/s---> si tenim que l'excitació en t=0 és 0, llavors...C-->Cs

Després, mitjançant uns exemples amb uns esquemes circuitals més que coneguts hem trobat la transformada de Laplace de les tensions de sortida de cadascun dels circuits , recordant que, segons on tingui la nostre funció de xarxa els pols, sabrem si serà una funció creixent (Semipla dret) o bé decreixent (semipla esquerra). 

1er Exemple:

Un cop trobada la transformada de laplace per trobar l'expresió vo(t) antitransformem utilitzant la descomposició en factors simples i trobem l'expressió de vo en funció del temps.

Per tal de trobar amb més exactitud quan durà exactament la fase transitòria mentres la nostra tensió no entre en RPS(si és que ho fa), haurem de trobar els factors concrets tau i K en cada cas concret, però en termes generals veïem que per a t= 5tau és més que suficient perquè en exponencials decreixents la resposta pròpia hagi desaparegut.

Per tant, tenim dos casos:

1. Circuits estables: Arrels en el semipla esquerra, al cap d'un cert temps que depèn de tau només tindrem la resposta forçada per com sigui l'excitació Vg a l'entrada. La pròpia es dispersa. Funcions decreixents tendint cap a 0.
2. Circuits inestables: Arrels en el semipla dret. No es dissipen, sinó que augmenten, funcions creixents tendint cap a infinit, encara que ho analitzem amb una excitació petita i en poc temps.

Transformada de Laplace

En la classe d'avui,que ha sigut molt rigurosament matemàtica, hem introduït el concepte de transformada de Laplace que ens servirà per saber quan dura la frase transitòria del nostre circuit abans d'arribar a la fase de règim permanent sinusoïdal o podrem saber si hi arriba o no.


                            

Definició Transformada Laplace d'una certa funcio F(t)

A continuació a través de la definició de transformada de Laplace d'una funció genèrica hem anat trobant una sèrie de funcions, les més comuns com a excitacions dels nostres circuits i hem realitzat "una taula" amb elles.
1) Excitació Vc
2) Exponencial decreixent
3) " Creixent
4) Vm·cos(t)
5) Vm·sin(t)
6) Delta de Dirac(Funció esglaó)

NOTA: Si tenim arrels del tipus (s-p), depenen si p es troba al semipla esquerra o al semipla dret podem dir que:

• Dret: Funcions decreixents amb el temps
• Esquerra: Funcions creixents amb el temps

Hem vist un exemple amb un circuit i hem també donat una mena de "circuits asimptòtics" per compravar si em Antitransformat correctament o no.

Finalment i això ens ha tranquil·litzat, hem vist que quan analitzem Inductàncies L aplicant Laplace obtindrem "LS"!
Sí! Com quan trobavem la funció de xarxa H(S) i veiem que canviavem L per LS!
Així que, no serà tant diferent al que havíem fet fins ara, segons el professor, a partir de la pròxima classe, ens trobarem més en el nostre terreny on ja hi estarem més còmodes, esperem que així sigui!



           

Pierre-Simon Laplace

Aplicant l'espectre freqüencial

En la classe d'avui hem començat amb un exemple de com trobar l'espectre freqüencia d'una tensió vg de senyal quadrada a l'entrada i hem observat que com més alta sigui la freqüència més abrupta serà la corba i menys s'assemblarà a una senoide. Hem vist que per realitzar aquests exercicis ens és molt útil treballar amb decibels micro volt ja que per trobar la sortida només hem de sumar-li a la entrada el guany en dB que ja sabem calcular de quan fèiem Bode.


Després ens hem  plantejat com poder dissenyar un circuit que enes permeti  trobar el valor mig d'un senyal.
Tot i que al principi pugui semblar molt difícil, hem anat procedint poc a poc per tal d'obtenir el resultat esperat.
Si ens fixem amb la Sèrie de Fourier en què descomposem la nostra senyal d'entrada veïem que el terme de freqüència 0, Co és en sí el valor mig de la senoide d'entrada, així que el que hem de fer és evitar que les altres senoides que en són suma apareixin al nostre circuit.

Lògicament no les podem eliminar del tot, però el que sí que podem fer és seleccionar una freqüència de tall del filtre "paso bajo" molt menor a la freqüència fonamental de la senyal d'entrada del nostre circuit.

SIGNAL/NOISE

Tot seguit, hem definit un nou concepte, el qüocient senyal/soroll, que ens dóna una idea de com d'efectiu és el nostre filtre i si queda molt de rastre de les senoides "paràsites" que volíem eliminar o no pas tant. Hem establert que per no ser un error important podíem despreciar una diferencia d'uns 30dB i en general 2 ordres de magnitud de diferència.

Per últim ens hem preguntat com poder d'un senyal periòdic el que sigui tenir a la sortida només la seva amplitud és a dir en DC.

Per això hem vist que, si aplicàvem una senoide amb una certa freqüència fo a la sortida necessàriament hi havia d'haver un senyal amb aquesta freqüència, per tant sembla com si haguèssim de treballar amb circuits no lineals. Però abans de creuar la frontera prohibida, que no ho farem, podríem tenir en compte un circuit conegut a electrònica com a un filtre de mig cicle amb un díode de manera que només tenim els semicicles positius de la senoide.

Finalment hem vist que per obtenir vo=vm(Amplitud de la senyal d'entrada) havíem  de montar un circuit "potent" combinant tot allò que hem aprés durant el curs, el circuit és el següent:

Circuits amb excitació periòdica. Jean Baptiste Joseph Fourier

En la classe d'avui hem vist com treure-li profit a les sèries de fourier apreses a càlcul avançat en circuits. Hem vist que mitjançant un espectre de freqüències podem descriure la font generadora vg(t) en un sumatori d'n termes, mitjançant l'aproximació per fourier i que serà més exacte com major sigui el nombre "n" de termes.

Fourier, a més, va definir que l'error quadràtic mitjà fruit d'utilitzar la seva aproximació era ajustable segons els n termes que possèssim.

Hem anomenat a la fo que acompanya el terme C1 del nostre sumatori freqüència fonamental, ja que totes les altres són múltiples d'aquesta. Així, també podem definir les tensions v1,v2,v3....vn en general com a harmònics, i més concretament, v1 com a harmònic fonamental.

Tot seguit hem vist com dur a terme la representació espectral en un senyal quadrat mitjançant les fòrmules donades per Fourier i les nocions que tenim de complexes per poder trobar el resultat.
A continuació, amb eles resultants obtinguts hem fet una taula on hem vist que per a n parells, els termes cn eren 0 i així amb l'angle, això en tot els parells. Així hem obtingut l'espectre de tensions quadrades.

MOLT BONIC, PERÒ ÉS BONA L'APROXIMACIÓ?

Per últim ens hem preguntat si l'aproximació era bona mitjançant un exemple on hem calculat la potència en una resistència Rl deguda en un cas només per un generador arbitràri, o en el segon cas per una font contínua(terme Co) i per, en aquest cas, 2 fonts alternes de freqüències fo i 2fo respectivament.
Hem demostrat llavors que només tenint n=2, l'error ja és d'un mínim 5% cosa que farà que sigui una fantàstica aproximació per facilitar-nos els càlculs en treballar amb excitacions periòdiques i ens permetrà "traduir" senyals quadrats,triangulars,....a senoides.

Jean Baptiste Joseph Fourier

Nous conceptes arrant de l'anàlisi pel traçat de Bode

En la classe d'avui, hem començat per un repàs del concepte de pics de ressonància, quan es donava (arrels complexes conjugades, és a dir, rho menor que 0,1.

Hem vist que amb aquesta condició, si calculàvem el guany en les arrels és a dir, en wo+rho·who i la seva conjugada, trobavem que en els dos ens quedava que el guany era el mateix del pic -3dB a aquestes w's caràcterístiques se'ls denomina de tall superior i inferior (vistes a física 1 sense explicar d'on sortien) i hem definit el Band Widht, l'ample de banda com la resta entre les dues.

                             

Un cop, arribats aquí hem trobat interessant i convenient tenir algun paràmetre per a calificar la qualitat del pic de ressonància, podem raonar, per exemple, que amb un ample de banda més petit, tindrem una sensibilitat, una qualitat major. Així doncs, el factor de qualitat és: Q=f/Bw


Per fer-ne un exemple, hem représ un anteriorment fet a classe i hem vist que com que cumplia que rho era menor que 0,1 podia tenir pics de ressonància, a continuació, hem fet el diagrama de Bode i hem comentat com representar-ho amb PSPICE degudament (triant un interval de freqüències que ens permeti veure que passa a l'esquerra i a la dreta de la freqüència característica del nostre circuit).


Per últim, hem introduït una nova unitat en què expressar el guany el dBmicroV, hem vist que ens queda una expressió similar a la que relacionava dBm amb dB (Pin, Pl). Ens queda la següent expressió:

             dBmicrovolt Vo=GdB+dBmicrovolt Vg

Hem acabat veient un exemple pràctic d'aplicació.

Aprofundint més en els traçats de Bode

En la classe d'avui, després d'un breu incís fet sobre l'aproximació de fases amb Bode, mostrant que enlloc de mostrar el salt de, per exemple 0 a pi/2 radians podem mostrar entre aquests dos una recta de tendència d'un cert pendent rad/dec o bé rad/oct.

Després mitjançant un exemple d'un filtre de pas baix amb una R i C conegudes hem representat gràficament l'amplitud i la fase en funció del log de la freqüència que també era coneguda. i hem avaluat l'expressió de guany en una freqüència situada molt a la dreta (2 dècades major que la de tall).

Al següent exemple sí que hem vist una nova cosa, que, quan canvíem la R per la C i a l'inrevés (Dibuix més a sota). Obtenim una funció de xarxa on, si les separem en  dos dels casos comentats anteriorment com a factors(en teníem 4), els dos en què la separem tenen la mateixa freqüència característica w1=w2=1/RC.
    

Al representar hem vist llavors que quan la freqüència era inferior a 1/RC només teníem la de pendent positiu, però si era major una s'anul·lava amb l'altre (Una de pendent +20db/dec, l'altra de -20dB/dec).

Hem vist que amb Bode ens seria fàcil també fer-ho si w1 fós diferent d'w2 seguint el mateix raonament.

POLINOMIS DE SEGON ORDRE

Per últim i la part més extensa de la classe ha estat anal·litzar el cas en que ens trobem polinomis de segon ordre en la funció de xarxa del nostre circuit i com realitzar-ne el traçat de Bode. Hem vist que hi trobem dos paràmetres claus, rho i wo que faran variar les arrels del nostre polinomi.

Hem distingit entre 4 casos i hem fet un exemple de l'últim veïent que trobavem un màxim en w=wo, anomenat pic de ressonància (pel seu símil sonor).

Corbes de resposta freqüencial

En la classe d'avui hem vist que si recordem el principi de curs quan vam aprendre a trobar la funció de xarxa característica d'un circuit concret i inclús classificar-les de manera que simplement veïent un circuit sabíem la resposta que n'obtindríem amb una certa excitació Vg.

Doncs, a partir d'aquesta expressió podem obtenir els traçats de Bode que ens mostraran la corba d'amplificació del circuit de modul |H|=|Vo|/|Vg|.

Per tal de poder-la dibuixar, un cop factoritzats els polinomis del denominador i numerador i trobades les arrels, hauríem de saber si té mínims, màxims, etc....és a dir, MOLT de càlcul. 

Per evitar això, Bode va proposar treballar amb una expressió logarítimica (una pel mòdul,una per l'angle) que ens estalviarà, encara que no ho sembli, molta feina alhora de trobar certs guanys en qualsevol punt.

 20log(H(jw)) -> log w

 argH(jw) -> log w

Per això, anomenem "zeros" a les arrels del numerador i "Pols" a les arrels del denominador.
Partint d'això podem establir uns diagrames P-Z i trobar les corbes, però enlloc de trobar una corba que complica el càlcul  trobarem una recta d'amplificació de cert pendent fàcil de trobar i de la qual podrem deduïr altres amplificacions a diferents punts.

Hem vist, mitjançants 4 factors (4 exemples en diferents tipus de funció de xarxa) i hem vist que quan ens és més útil Bode és quan tenim expressions del tipus:

-On,si:

• W<<w     El guany en dB=0

• W>>w     Decreix en el cas proposat, en 20 dB.

Hem compravat que l'error és mínim en expressions d'aquest tipus pel que fa a l'amplificació, pel que fa a l'angle sí que hi ha errors importants.

Traçats de Bode/Aproximació Real

Usos del transformador perfecte aplicats a exemples pràctics

Avui, hem començat la classe amb una reflexió sobre la situació actual de l'universitat pública, una situació molt preocupant portava per una colla d'ineptes i corruptes rectors de les universitats públiques en generals que s'han posat al servei d'un govern privatitzador i liberal a més no poder, totalment d'acord amb el professor.

Després, tornant a circuits lineals hem comentat les principials tres aplicacions que li donarem al transformador perfecte, que són:

1. Canviar Voltatges i Intensitats

Hem parlat del cas més correct, 220Volts eficaços amb una Ief corresponent i una Rl de sortida que podia tractar-se de qualsevol aparell electrodomèstic de casa, per exemple. Hem vist que amb una relació de n=1000 podíem augmentar significativament Vef. A partir d'aquí i el càlcul de la potència Pl i les pèrdues hem vist que per tal de minimitzar les pèrdues podem fer dues coses, o bé en paral·lel al inductor hi col·loquem un condensador que ens permeti que a una freqüència constant poguem seguir les equacions del transformador o bé fem l'inductor molt gros per què quasi no hi circuli corrents, hem vist que és més econòmica i pràctica la primera via.

2. Canviar Impedàncies.

Per tal de variar el valor de les impedàncies depenen si volem una Rl>Rin o bé Rl<Rin haurem de agafar una relació de transformació n concreta i per això, si volem augmentar la relació doncs buscarem un coeficient de permeabilitat magnètic major i si busquem una Rl<Rin llavors podem girar el trafo, és a dir, el primari i el secundari posar-los al revés fent la relació inversa.

3. Aïllament elèctric entre primari i secundari.

Per últim hem vist per a què serveix posar les mateixes espires al primari que al secundari,hem vist que tots els aparells com telèfons, modems etc en porten, per tal d'evitar descàrregues al secundari, és un element de seguretat indispensable.

Finalment, hem introduït el concepte del Teorema de la Màxima Transmissió de Potència (TMTP) que el que ens diu és que, per tal de transmetre la Pl màx el resistor del generador ha de ser igual que el de la sortida.

Vist en general,un cop fet el CTF i el Thevenin equivalent,amb inductàncies i transformadors hem vist que la inductància de sortida era la conjuda de la de Thevenin.

De l'idealitat a la perfecció

En la classe d'avui hem començat amb un breu resum sobre el que vam veure en la darrera classe, el transformador ideal, i tot mitjançant un exemple present ja en els exercicis per entregar aquesta setmana hem pogut veure el model que més s'hi assembla a la realitat.

EL TRANSFORMADOR PERFECTE

Com podem observar ja hem passat d'incloure l'adjectiu ideal a perfecte, tot i això el model circuital del transformador perfecte és, pràcticament igual al de l'ideal (per alguna cosa és el que més s'hi assembla). Així doncs ens queda el següent model circuital:

L1=Inductància

Si ens fixem amb detall en el model circuital obtingut veurem que, a diferència del seu antecessor purament teòric, aquest no pot funcionar en DC ja que la bobina seria un curtcircuit i no es cumplirien les equacions plantejades en el TI.

SIMBOLOGIA:

En el nou circuit la "n" no podrà ser qualsevol sino que vindrà definida per:


                

Tot seguit hem vist que havíem d'utilitzar ferrita (material amb un alt coeficient de permeabilitat magnètica però aïllant) ja que si utilitzàvem, per exemple ferro, estàvem creant una bobina d'una sola espira que produïa un curcircuit que anul·lava l'efecte del transformador com un d'ideal.

Després d'incedir més en l'electromagnetisme que hi està involucrat hem justificat la fòrmula donada més amunt.
Finalment, després d'uns exemples hem parlat sobre com s'apliquen els transformadors a la vida diària, per exemple, en una tenda els llibres tenen una part del transformador en el xip que porten perquè si algu intentés robar-lo al completar-se el transformador amb l'arc de la porta, pitaria. A caixa el que ens fan és amb un fort camp magnètic incidit en el xip, cremar el fusible que porta per evitar que piti (es podria fer amb un fort electroimant).

Espero que no en fem mai mal ús d'aquests coneixements.

                                   

En la classe d'avui i, després d'un resum força extés sobre la classe del darrer dia que recordem que tractava d'una línia de transmissió. Hem començat recordant doncs la interessant fòrmula en què obteníem la relacio entre Pin i Pl amb dBm's relacionat amb el guany en dB, la fòrmula era la següent:

 PL(dBm)=Pin(dBm)+G(dB)

Després hem vist alguns exemples amb la línia de transmissio treballant amb un dels cables coaxials més comuns, l'RG58.

A continuació hem introduït una reflexió molt important:

I si la nostra resistència de sortida Rl NO coincideix amb el paràmetre característic Zo del cable coaxial triat? Hauríem de trobar una manera d'enganyar al circuit i fer que ell veiés una resistència diferent del valor real d'aquesta,no? I això es pot fer? Doncs sí, amb un nou component elèctric anomenat TRANSFORMADOR.

1) V1=n·V2
2) n·I1=-I2

Així hem introduït el transformador i em vist mitjançant uns exemples i un parell d'equacions descrites just amunt amb què no només podem fer veure al circuit que el valor d'R és un diferent si no que podem substituir bobines per condensadors.

Sembla tot fantàstic no? Algun incovenient? Doncs, un transformador ideal o CPI(Conversor positiu impedàncies)no existeix com a tal, hi hauran unes certes mancances a la realitat, però com que avui hem exercit de rigurosos teòrics, ho deixarem així.

El resum per dur a terme el procés de "variar" el valor de la R és el següent:

1)Traslladar al primari la resistència de sortida (Zl)Tot seguint les fòrmules del trafo.

2)Realitzem operacions per trobar el valor de ZL

3)Destransformem i trobem allò que buscàvem.

Transformador amb les bobines primària i secundària

Plantejant un problema real amb allò aprés fins ara

En la classe d'avui, després d'un breu repàs d'allò vist en la classe anterior hem plantejat un problema corrent i no gens fàcil de solucionar, com ja ha mencionat el professor:

Com "apropar" un generador sinusoïdal que podem assimilar a una antena i una resistència que podria ser perfectament la d'entrada del nostre televisió a molts metres de distància.
Com ja vam esmentar en la primera classe, quan la longitud del nostre circuit L és major que c/f (velocitat de la llum entre la freqüència a que treballa) no podríem aplicar Kirchoff perquè no es cumplirien les nostres previsions.

Un cop plantejat el problema, els experts ens recomanen que el resolguem amb el següent esquema circuital(l'hem anomenat circuit clau) i ens diuen que, donat la seva fitxa tècnica, podrem comprovar que, efectivament resol el problema.

El circuit és el següent:

Circuit Clau

Un cop comprovat la seva fitxa tècnica matemàticament, hem plantejat com portar-lo a la realitzat i és per això que hem analitzat un model de plaques metàliques paral·leles amb un espai entre si i una certa llargada i amplitud, així hem arribant, tot passant per les fòrmules de inductància i capacitat al més pur estil de l'electromagnetisme.
També hem vist, comparant la nostra idea amb els cables coaxials que s'utilitzen per a realitzar aquestes transmissions a certa distància entre Vg i R i hem vist les nostres mancances.

Però també hem vist que fins i tot amb els coaxials a molta distància perden efectivitat ja que la potència perduda a través d'ell és tan grossa que elimina totalment l'efecte de guany de l'amplificador. Per això hem dit que serà, tot i que al principi no ho sembli més factible transmetre a partir d'ones radioelèctriques.

Potència (II)

En la classe d'aquest darrer dijous hem comentat altres detalls a tenir en compte alhora de calcular potències veient alhora exemples de cada aplicació en circuits, aquí en fem un resum dividit en casos.

1. Sinusoïdes de la mateixa freqüència: NO apliquem superposició, utilitzem molts càlculs.
2. Sinusoïdes a diferent freqüència: PODEM utilitzar superposició. Mateixes expressions
3. Arbitràries: S'ha d'anar amb compte, sempre buscant el valor eficaç (Vrms) de la sortida.

A més, hem demostrat matemàticament que els resistors són els únics components que dissipen potència (dels treballats fins ara) i s'ha definit el voltatge eficaç (fòrmula en l'anterior entrada).


Per acabar hem introduït una nova unitat que alhora d'expressar potència en la nostra vessant utilitzarem més, el decibel (dB) i el dBm, del famós Graham Bell.
Hem vist la relació logarítmica que va plantejar i hem fet un parell de taules amb els valors W/dB i W/dBm (basats en quan de grans són respecte 1 mW), respectivament.

Conversió a dB (E2 i E1 en Watts)

Potència (I)

En la classe del darrer dilluns vam parlar del concepte de potència que vam  veure que per treballar amb certs dispositius, per exemple l'amplificador operacional tant utilitzat en els nostres últims dissenys necessitem limitar la intensitat que hi passa a través a no més de 30mA. 

Per fer això és important saber calcular la potència per a que això es compleixi. Abans de determinar com calcular-la vam parlar dels descriptors parcials de tensió i com calcular-los. Vam veure que es,el valor mig tractava d'una integral en un cert interval de temps(t1-t2) sobre una gràfica V/t, és a dir, una àrea. 

Vam distingir diversos casos, segons com resoldre'ls:

1. Amb w=0 vam veure que els condensadors i les bobines no dissipaven cap potència i tota la del circuit era igual a la de la suma de les potències de cada resistor.
2. Vam veure que amb excitació sinusoïdal, havíem de recorrer al CTF. Totes les tensions són de la mateixa forma, així que podem expresar la potència mitjana en funció dels seus fasors.
3. Potència a circuits amb AO's. Vam calcular la Pm en funció de la intensitat llindar que marcava les característiques del AO

NOTA: Alhora de calcular les potències en un circuit NO podem aplicar superposició.

A.O's COM A COMPARADORS

El darrer dia de classe el vam acabar introduint breument la idea que els A.O's poden actuar com a comparadors depenen que es doni una certa condició l'A.O salta a saturació positiva o bé a negativa.

En la classe d'aquest dijous hem vist que això ho podem fer mitjançant el circuit següent:

on:  Recordem que si a la funció signum(v+-v-), v+ era major, l'A.O saltava a saturació positiva i si passava el contrari, a negativa.

Com es pot apreciar al circuit podem comprovar que passa això posant un díode LED en sèrie amb una resistència a la sortida polaritzat de tal manera que només s'il·lumini quan passi una de les dues coses o bé, també podríem posar dos LED's un pol·laritzat en un sentit i l'altre en el contrari, això si, per evitar errors en la lectura seria adeqüat que irradiessin colors diferents.

També vam veure el concepte de cicle de treball de tensions bipolars i la vam definir com el temps durant el qual tenim el díode en ON dividit pel període i per tal d'expressar-ho en tant per cent, multiplicat per cent:

                      T= (Ton/Tper.)·100

Com a últim exemple d'aquest apartat vam poder veure que en un circuit amplificador format per dues tensions v1 i v2, connectades a un seguidor de tensió connectats en cascada a través d'una resistència de 10k amb un amplificador amb el terminal positiu a un divisor de tensió com en la figura anterior, si a la sortida vo i connectavem un LED i suposàvem els 4 possibles valors combinats de v1 (recordant les taules de la veritat vistes al batxillerat a tecnologia) veïem com actuava com una porta lògica NAND (AND inversa). Aquí està el circuit:

Detalls en A.O's

Per últim vam comentar els detalls a tenir en compte alhora de treballar amb A.O's.
L'estabilitat és un punt a tenir en compte, aquí vam distingir en el que era una funció de xarxa estable i quina no, i vam concloure per exemple que la funcio H(S)=1/S-a no era estable ja que si recorríem a la seva expressió diferencial, per poc que canvies Vo es produïa un brusc augment.

Al final de la classe vam plantejar que per tal de ser més competitius alhora de plantejar circuits hauríem de ser capaços de treballar amb alimentació unipolar per estalviar-nos piles i bateries i fer més atractiu el nostre producte. Vam veure que podem aconseguir el mateix resultat que amb dues procedint correctament.

Disseny modular

Després de la setmana santa, en la primera classe hem comencçat amb un repàs molt necessàri sobre el que hem vist fins ara dels amplificadors operacions i les seves aplicacions alhora de dissenyar els nostres circuits.

Arribats a aquest punt hem plantejat que alhora de ser més eficaços i concisos alhora de obtenir un resultat desitjat en un circuit podíem agrupar només els tipus de circuits amb AO's bàsics per realitzar operacions lineals , formant una biblioteca minimalista de blocs funcionals que, mitjançant la unió entre si ens facilitessin la solució d'un determinat problema plantejat. Hem vist que la nostra biblioteca només cal que tingui 5 blocs bàsics:

1. Un bloc que ens permeti que el voltatge de sortida sigui proporcional al d'entrada a través d'una constant genèrica K--> Vo=k·Vin. Com hem treballat a la teoria hem vist que això ens ho permetia fer el NO INVERSOR on la k seria 1+R2/R1 de manera que podríem ajustar-la variant el valor de les resistències.
2. Un bloc que ens permeti multiplicar també per una constant K però aquest cop, si aquesta està compresa entre 0 i 1. Per realitzar aquest bloc utilitzaríem el ja més que conegut DIVISOR DE TENSIÓ i, si volguessim assegurar al nostre client/a que a la tensió de sortida Vo del DdT no estarà alterada afegiríem a continuació connectat en cascada el SEGUIDOR DE TENSIÓ.
3. Per tal d'estalviar-nos haver d'afegir un sumador, necessitarem un bloc canvi de signe que, com ve sabem, el circuit INVERSOR ens permet  realitzar aquesta operació.
4. També ens sera útil un bloc que ens permeti restar tensions i, en conseqüència si l'hi apliquem el canvi de signe, sumar-les. Per tant, utilitzarem el circuit RESTADOR.
5. I, finalment, necessitarem un bloc integrador de manera que a partir de la característica H(s) de l'integrador: 1/S poguem trobar la tensió de sortida. A partir d'aquest podem deduïr fàcilment com serà H(s) del derivador sense necessitat d'afegir-lo als blocs bàsics.

Un cop vists els blocs funcionals bàsics, hem vist un parell d'exemples on se'ns proposava una determinada Vo de sortida (que si recordem els primers dies de classe SEMPRE és f(Vg1+Vg2+..Vgn)) i amb els blocs bàsics havíem d'aconseguir la sortida.

Mitjançant aquests exemples hem comprovat que, donada una funció de xarxa qualsevol, som capaços d'obtenir un esquema circuital de blocs trobant solució a la sortida Vo. Sempre procedirem igual donana H(S), aïllant el terme d'S de major grau que està multiplicant a Vo.

Per últim hem introduït el funcionament dels AO's com a comparadors veient que també podrà donar-se el cas en què el CCV (v+=v-) no sigui cert però aquí s'ha acabat el temps.

Gràfica Zones de treball AO

LABORATORI 22/03/13

Aquest dijous al laboratori hem posat a prova amb el que hem aprés a classe per tal de poder dissenyar un circuit amplificador que com vam dir a l'hipòtesi per k=3 ens amplificava per 3 la tensió sinusoidal d'entrada.


Al laboratori doncs hem muntat el següent circuit a la protoboard amb un amplificador operacion Tl081 i una resistència de 10k i una de 20k, que hem substituït per dues de 10k ja que 20 k no és un valor comercial. Aquest és el montatge fet a la protoboard:


1.DISSENY AMPLIFICADOR NO INVERSOR

• Resultat gràfic amb el PicoScope (Vg=1V i 1kHz de freqüència/Vo=3V i mateixa freq.)

2.AMPLIFICADOR AMB GUANY AJUSTABLE PER POTENCIÒMETRE

Un cop comprovat l'exemple anterior, el que volem obtenir és un guany ajustable per l'usuari i per això necessitem substituir al nostre circuits les resistències per un potenciòmetre ajustable (Comentat el funcionament en l'entrada anterior). L'esquema teòric és el següent.

• Resultat alpha= 1/2 Amplificació 2V

• Resultat PicoScope per alfa=0 (Amplificació "infinita"-->No realimentació)

• Resultat Picoscope per alfa=1(Vg=Vo Superposades)

3.GENERADOR SINUSOÏDAL:

Un cop comprovats els dos resultats anteriors ja estem en condicions de dissenyar el nostre propi generador sinusoïdal. Amb una excitació Vg nula obtindrem a la sortida una sinusoide d'una freqüència teòrica d'uns 1942Hz amb les R=10k i C=8'2nF.

• Resultat Picoscope:

NOTA: Tot el contingut de laboratori està explicat amb molt més deteniment a la llibreta de laboratori al seu apartat pertinent.